Graph Searching
그래프에서 두 노드 사이에 path를 찾기 위해서는 두 노드사이의 edge들을 찾아서 연결되는지 확인을 해야 하는데 이러한 동작을 하는 방식으로 대표적으로 DFS와 BFS가 있다.
- DFS
DFS는 깊이 우선 방식으로 모든 노드들을 다 방문할 때 현재 노드에서 edge를 통해 갈 수 있는 모든 노드들을 stack에 저장을 한다.
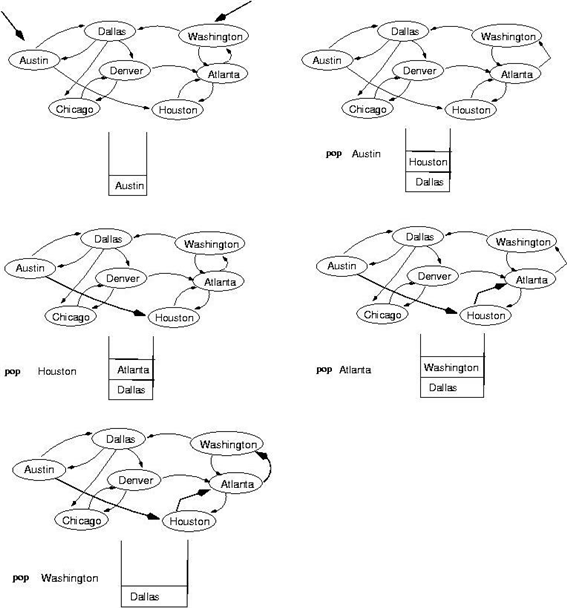
그리고 stack에 pop을 하여 pop이 된 위치에서 갈 수 있는 모든 노드들을 바로 stack에 append 해준다.
만약 이전에 방문했던 노드가 있다면 해당 노드는 다시 방문할 필요가 없으므로 이전에 방문을 하였는지 따로 확인할 수 있는 mark가 필요하다.
이렇게 stack의 모든 노드들이 없어지거나 원하는 노드에 방문할 때까지 반복을 하여 만약 도착에 성공한다면 해당하는 과정을 path로 하면 되고, stack이 비게 된다면 둘 사이에 path가 존재하지 않아 방문을 할 수 없다는 뜻으로 생각하면 된다.
template<class VertexType>
void GetToVertices(VertexType vertex, QueType<VertexType>& adjVertices) {
int fromIndex;
int toIndex;
fromIndex = IndexIs(vertices, vertex);
for (toIndex = 0; toIndex < numVertices; toIndex++)
if (edges[fromIndex][toIndex] != NULL_EDGE)
adjVertices.Enqueue(vertices[toIndex]);
}
template<class VertexType>
void DepthFirstSearch(GraphType<VertexType> graph, VertexType startVertex, VertexType endVertex) {
StackType<VertexType> stack;
QueType<VertexType> vertexQ;
bool found = false;
VertexType vertex;
VertexType item;
graph.ClearMarks();
stack.Push(startVertex);
do {
stack.Pop(vertex);
if (vertex == endVertex) {
found = true;
}
else {
if (!graph.IsMarked(vertex)) {
graph.MarkVertex(vertex);
graph.GetToVertices(vertex, vertexQ);
while (!vertexQ.IsEmpty()) {
vertexQ.Dequeue(item);
if (!graph.IsMarked(item))
stack.Push(item);
}
}
}
} while (!stack.IsEmpty() && !found);
if (!found)
cout << "Path not found." << endl;
}
동일한 내용을 파이썬으로 짜면 다음과 같다.
def depth_first_search(graph, startVertex, endVertex):
stack = StackType()
vertexQ = QueType()
found = False
graph.clear_marks()
stack.push(startVertex)
vertex = stack.top()
stack.pop()
if vertex == endVertex:
print(vertex)
found = True
else:
if not graph.is_marked(vertex):
graph.mark_vertex(vertex)
print(vertex)
graph.get_to_vertices(vertex,vertexQ)
while not vertexQ.is_empty():
item=vertexQ.dequeue()
if not graph.is_marked(item):
stack.push(item)
while not stack.is_empty() and not found:
vertex = stack.top()
stack.pop()
if vertex == endVertex:
print(vertex)
found = True
else:
if not graph.is_marked(vertex):
graph.mark_vertex(vertex)
print(vertex)
graph.get_to_vertices(vertex,vertexQ)
while not vertexQ.is_empty():
item = vertexQ.dequeue()
if not graph.is_marked(item):
stack.push(item)
if not found:
print("Path not found.")
- BFS
BFS는 너비 우선 방식으로 모든 노드들을 다 방문할 때 현재 노드에서 edge를 통해 갈 수 있는 모든 노드들을 먼저 다 확인을 한 다음다음 노드들 에서 갈 수 있는 모든 노드를 확인하는 방법으로 찾고자 하는 노드를 찾을 때까지 반복하는 방식이다.
이러한 방식은 먼저 확인한 노드를 먼저 탐색해야 하므로 FIFO구조로 queue를 활용하면 된다.

DFS와 마찬가지로 똑같은 노드를 중복해서 확인하면 메모리적으로 손해임으로 방문했는지 구분할 수 있는 mark가 따로 존재해야 한다.
template<class VertexType>
void BreadthFirstSearch(GraphType<VertexType> graph, VertexType startVertex, VertexType endVertex); {
QueType<VertexType> queue;
QueType<VertexType> vertexQ;
bool found = false;
VertexType vertex;
VertexType item;
graph.ClearMarks();
queue.Enqueue(startVertex);
do {
queue.Dequeue(vertex);
if (vertex == endVertex)
found = true;
else {
if (!graph.IsMarked(vertex)) {
graph.MarkVertex(vertex);
graph.GetToVertices(vertex, vertexQ);
while (!vertxQ.IsEmpty()) {
vertexQ.Dequeue(item);
if (!graph.IsMarked(item))
queue.Enqueue(item);
}
}
}
} while (!queue.IsEmpty() && !found);
if (!found)
cout << "Path not found" << endl;
}
동일한 과정을 파이썬으로 짜면 다음과 같다.
def breadth_first_search(graph, startVertex, endVertex):
queue = QueType()
vertexQ = QueType()
found = False
graph.clear_marks()
queue.enqueue(startVertex)
vertex = queue.dequeue()
if vertex == endVertex:
print(vertex)
found = True
else:
if not graph.is_marked(vertex):
graph.mark_vertex(vertex)
print(vertex)
graph.get_to_vertices(vertex,vertexQ)
while not vertexQ.is_empty():
item = vertexQ.dequeue()
if not graph.is_marked(item):
queue.enqueue(item)
while not queue.is_empty() and not found:
vertex = queue.dequeue()
if vertex == endVertex:
print(vertex)
found = True
else:
if not graph.is_marked(vertex):
graph.mark_vertex(vertex)
print(vertex)
graph.get_to_vertices(vertex,vertexQ)
while not vertexQ.is_empty():
item = vertexQ.dequeue()
if not graph.is_marked(item):
queue.enqueue(item)
if not found:
print("Path not found.")
이렇게 큐의 모든 노드들이 없어지지 않고 원하는 노드에 방문할 때까지 반복을 하여 만약 도착에 성공한다면 두 노드사이에 path가 존재하는 것이고 만약 큐의 원소가 없으면 두 노드 사이에 path가 존재하지 않는 것이다.
이제 graph searching을 하여 path가 있는 것을 확인했다면 두 노드를 연결하는 가장 최적의 path를 구해야한다.
이는 상황에 따라 edge의 weight가 가장 큰 경우가 될 수도 있고, 가장 작은 경우가 될 수도 있어 상황에 따라 적절한 path를 골라야한다.
이때 최적의 path를 구하기 위한 알고리즘으로는 Dijkstra's algorithm, Bellman-Ford algorithm등 다양한 알고리즘이 존재한다.
'컴퓨터 > 자료구조' 카테고리의 다른 글
| 자료구조 - Searching (0) | 2023.12.02 |
|---|---|
| 자료구조 - Sorting (1) | 2023.12.02 |
| 자료구조 - 그래프 (1) | 2023.11.30 |
| 자료구조 - 우선순위 큐(Priority Queue) (0) | 2023.11.29 |
| 자료구조 - Heap (1) | 2023.11.29 |


