그래프
그래프는 vertex들의 집합으로 각각의 vertex를 연결하는 edge가 존재하여 vertex 간의 관계를 표현한다.
그래프는 G = (V, E) 형태로 표현되는데 여기서 V는 vertex들의 집합으로 유한하고 비어있지 않고, E는 edge들의 집합을 의미한다.
edge가 있을 때 vertex간의 방향이 존재할 수도 있고 존재하지 않을 수도 있다.
만약 vertex간의 방향이 존재하지 않는다면 undirected graph라고 하고 연결되어 있는 순서가 중요하지 않게 된다.
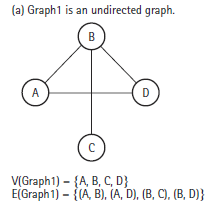
반면 vertex간의 방향이 존재한다면 directed graph라고 하고 연결되는 순서가 중요해져서 만약 1번 vertex와 3번 vertex가 있을 때 1 -> 3으로만 edge가 존재할 경우 3에서 1로는 이동할 수가 없다.
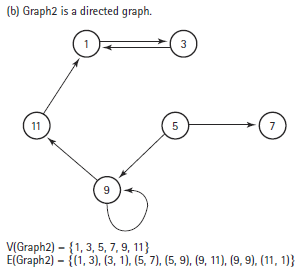
트리의 경우는 directed graph의 한 종류로 자기 자신으로 연결된 edge가 없고, cycle구조가 없으며, 하나의 vertex에서 나가는 방향은 상관없지만 들어오는 방향의 edge는 하나만 존재하고, 모든 vertex가 연결된 graph를 뜻한다.
edge로 연결되어있는 vertex를 adjacent nodes라고 하고 방향이 있는 경우 1 -> 2인 경우 1 is adjacent to 2 and 2 is adjacent from 1이라고 한다.
Weighted Graph
만약 그래프의 edge에 가중치가 존재한다면 이를 weighted graph라고 한다.
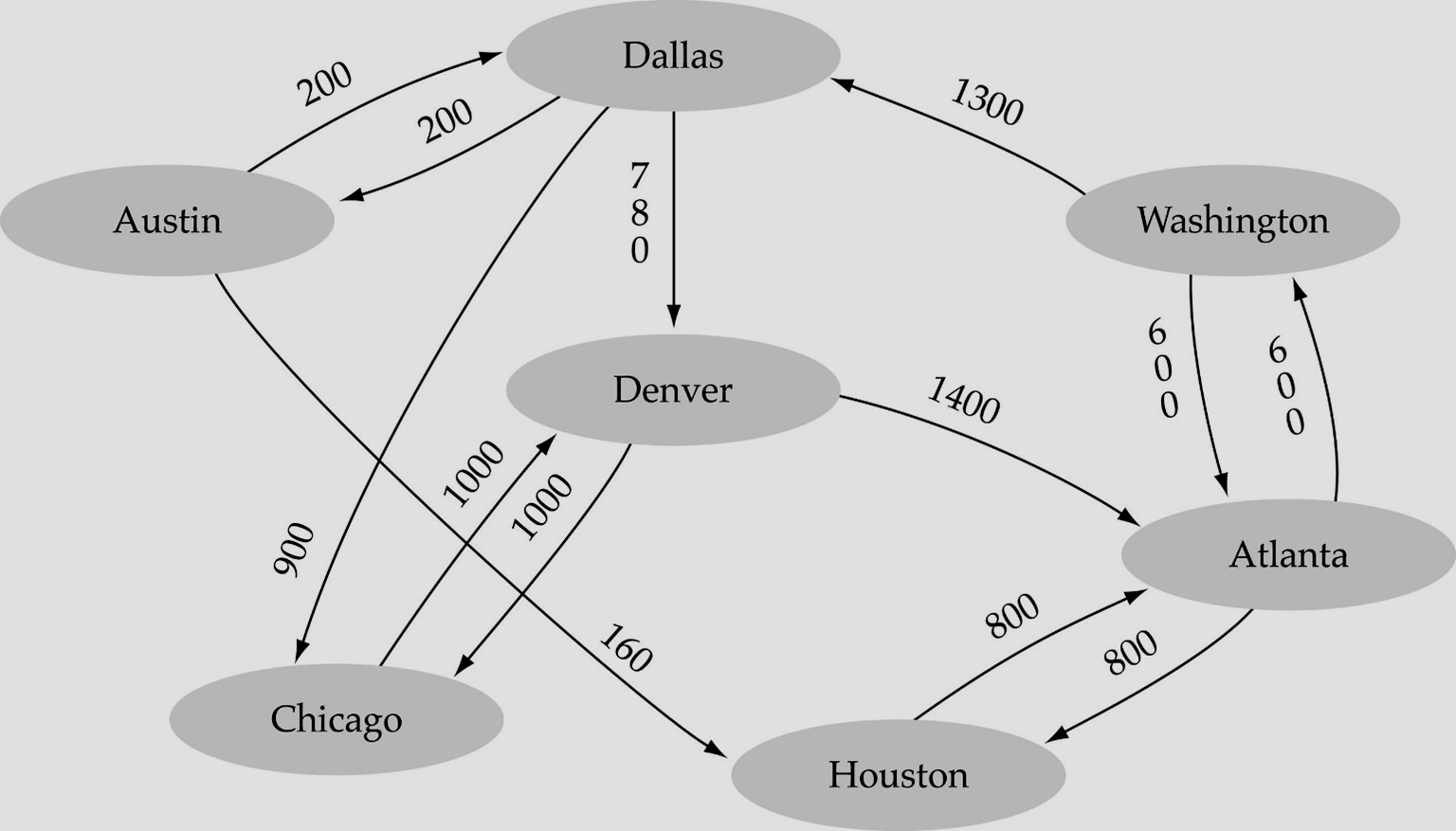
weighted graph를 저장하기 위해서는 2차원 배열을 사용하여 각각의 값을 graph[a][b] = a vertex에서 b vertex로 이동할 때의 가중치 형태로 저장을 하면 된다.
다만 각각의 vertex이름이 숫자가 아니기 때문에 1차원 배열로서 배열의 인덱스에 해당하는 값을 따로 만들어줘야 한다.
위의 그래프를 이차원 배열을 통해 표현하면 아래와 같이 만들 수 있다.
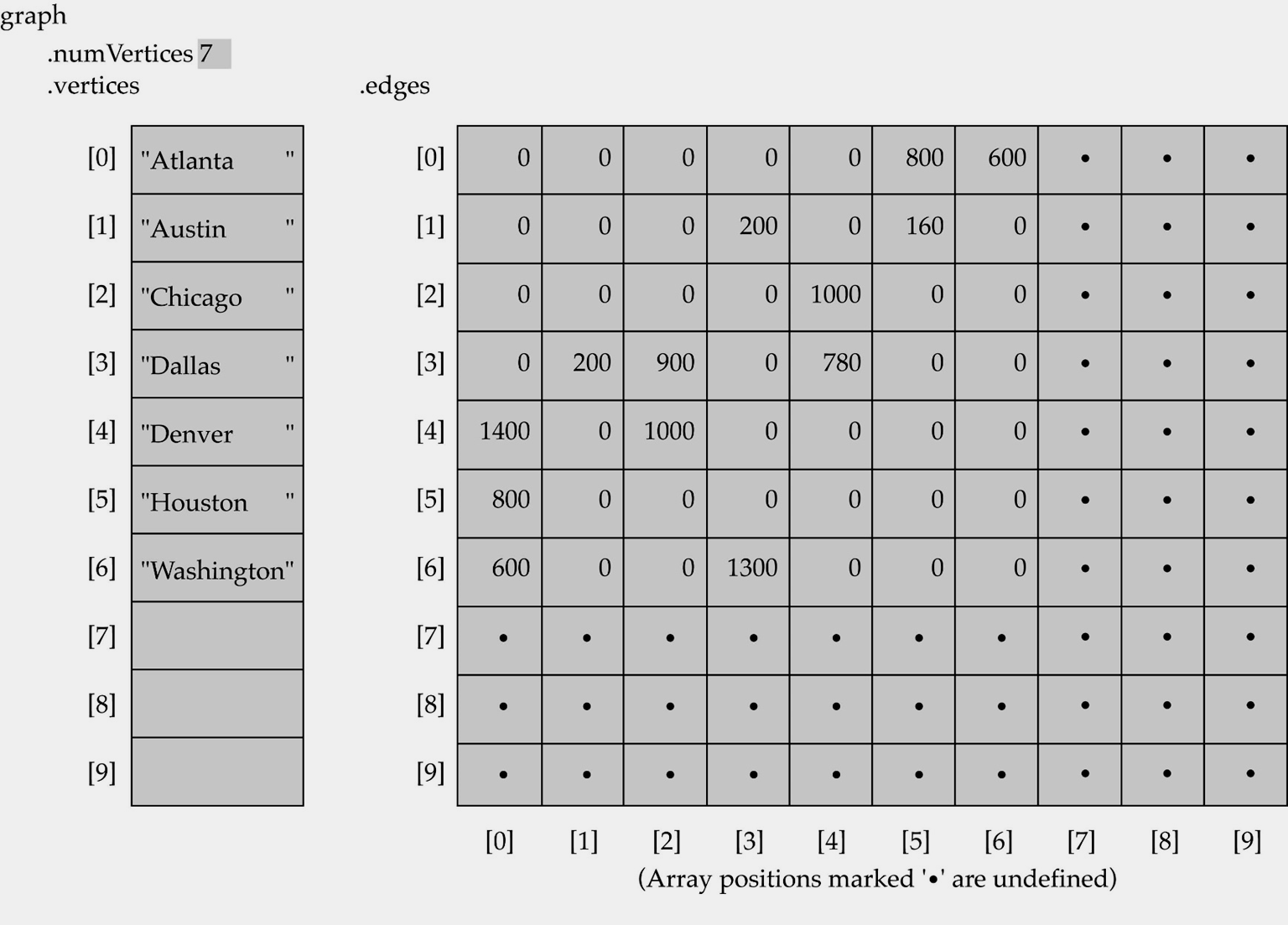
template<class VertexType>
void AddVertex(VertexType vertex) {
vertices[numVertices] = vertex;
for (int index = 0; index < numVertices; index++) {
edges[numVertices][index] = NULL_EDGE;
edges[index][numVertices] = NULL_EDGE;
}
numVertices++;
}
template<class VertexType>
int IndexIs(VertexType* vertices, VertexType vertex) {
int index = 0;
while (!(vertex == vertices[index]))
index++;
return index;
}
template<class VertexType>
void AddEdge(VertexType fromVertex, VertexType toVertex, int weight) {
int row;
int col;
row = IndexIs(vertices, fromVertex);
col = IndexIs(vertices, toVertex);
edges[row][col] = weight;
}
이를 파이썬으로 구현하면 다음과 같이 짤 수 있다.
class GraphType:
def __init__(self, maxV=50):
self.numVertices = 0
self.maxVertices = maxV
self.vertices = [None] * maxV
self.edges = [[NULL_EDGE] * maxV for _ in range(maxV)]
self.marks = [None] * maxV
def add_vertex(self, vertex):
self.vertices[self.numVertices] = vertex
for i in range(self.numVertices):
self.edges[self.numVertices][i] = NULL_EDGE
self.edges[i][self.numVertices] = NULL_EDGE
self.numVertices += 1
def add_edge(self, fromVertex, toVertex, weight):
row = index_is(self.vertices,fromVertex)
col = index_is(self.vertices,toVertex)
self.edges[row][col] = weight
def weight_is(self, fromVertex, toVertex):
row = index_is(self.vertices,fromVertex)
col = index_is(self.vertices,toVertex)
return self.edges[row][col]
def get_to_vertices(self, vertex, adjVertices):
fromindex=index_is(self.vertices,vertex)
for i in range(self.numVertices):
if self.edges[fromindex][i] != NULL_EDGE:
adjVertices.enqueue(self.vertices[i])
def clear_marks(self):
self.marks = [None] * self.maxVertices
def is_marked(self, vertex):
index = index_is(self.vertices,vertex)
if self.marks[index] == 1:
return True
else:
return False
def mark_vertex(self, vertex):
index = index_is(self.vertices,vertex)
self.marks[index] = 1
def delete_edge(self, fromVertex, toVertex):
row = index_is(self.vertices,fromVertex)
col = index_is(self.vertices,toVertex)
self.edges[row][col] = NULL_EDGE
graph에 vertex를 삽입하는 방법은 먼저 위의 방법처럼 새로운 값이 입력되면 vertex값이 저장되어 있는 1차원 배열에 해당하는 이름을 넣어준다.
그 후 기존에 있던 vertex와의 edge가 생길 수 있는 모든 영역에 NULL값을 입력해 줘서 새로운 vertex와 기존의 vertex사이의 weight를 입력해 줄 수 있게 한다.
그리고 graph에 edge를 삽입하게 되면 어떤 a vertex에서 b vertex로 edge가 생긴다고 했을 때 a와 b가 의미하는 index 번호를 찾아 해당하는 위치에 weight값을 삽입하면 된다.
다만 이러한 방법은 vertex 수에 비해 edge의 수가 적을 경우 vertex사이에 edge가 없는 경우가 많아 대부분의 weight가 0인 것을 볼 수 있다.
즉, 메모리를 엄청 많이 사용하지만 실질적으로 유용한 값을 가지고 있는 메모리는 별로 되지 않아 비효율 적이다.
따라서 이러한 방법 대신에 Linked List를 통해서도 graph를 구현할 수 있다.
Linked List를 통해 graph를 구현하는 방법은 1차원 배열로서 배열의 인덱스에 해당하는 값을 만들어주고, 각각의 vertex에서 edge들을 연결된 부분에 연결해 주면 된다.
다만 Linked List로 구현할 때는 연결되지 않은 edge가 많을 때 유용하고 만약 edge로 대부분 연결되어 있다면 배열을 사용하였을때 없었던 다음 노드를 가리키는 부분이 늘어나기 때문에 불필요한 메모리 사용이 많아져 오히려 비효율적이게 된다.

'컴퓨터 > 자료구조' 카테고리의 다른 글
| 자료구조 - Sorting (1) | 2023.12.02 |
|---|---|
| 자료구조 - DFS & BFS (Graph Searching) (1) | 2023.11.30 |
| 자료구조 - 우선순위 큐(Priority Queue) (0) | 2023.11.29 |
| 자료구조 - Heap (1) | 2023.11.29 |
| 자료구조 - 트리 (1) | 2023.11.28 |


