Heap
Heap은 이진트리에서 리프 노드를 제외하고 빠져있는 부분이 없는 complete binary tree 모양을 가지고, 모든 노드의 자식 노드는 자기 자신의 값보다 작은 값을 가지고 있는 순서 조건을 만족하는 트리이다.
일반적으로 Heap은 자식 노드들이 항상 부모 노드보다 작기 때문에 루트에 가장 큰 원소가 들어가 max-heap이라고 한다.
하지만 반대로 부모 노드가 항상 작게도 Heap을 구현할 수 있는데 이러한 경우는 min-heap이라고 한다.
Heap은 complete binary tree이기 때문에 중간에 비어있는 노드가 있으면 안돼서 일반적인 tree처럼 Linked List로 구현하는 것보다 array로 구현하는 것이 더 쉽다.
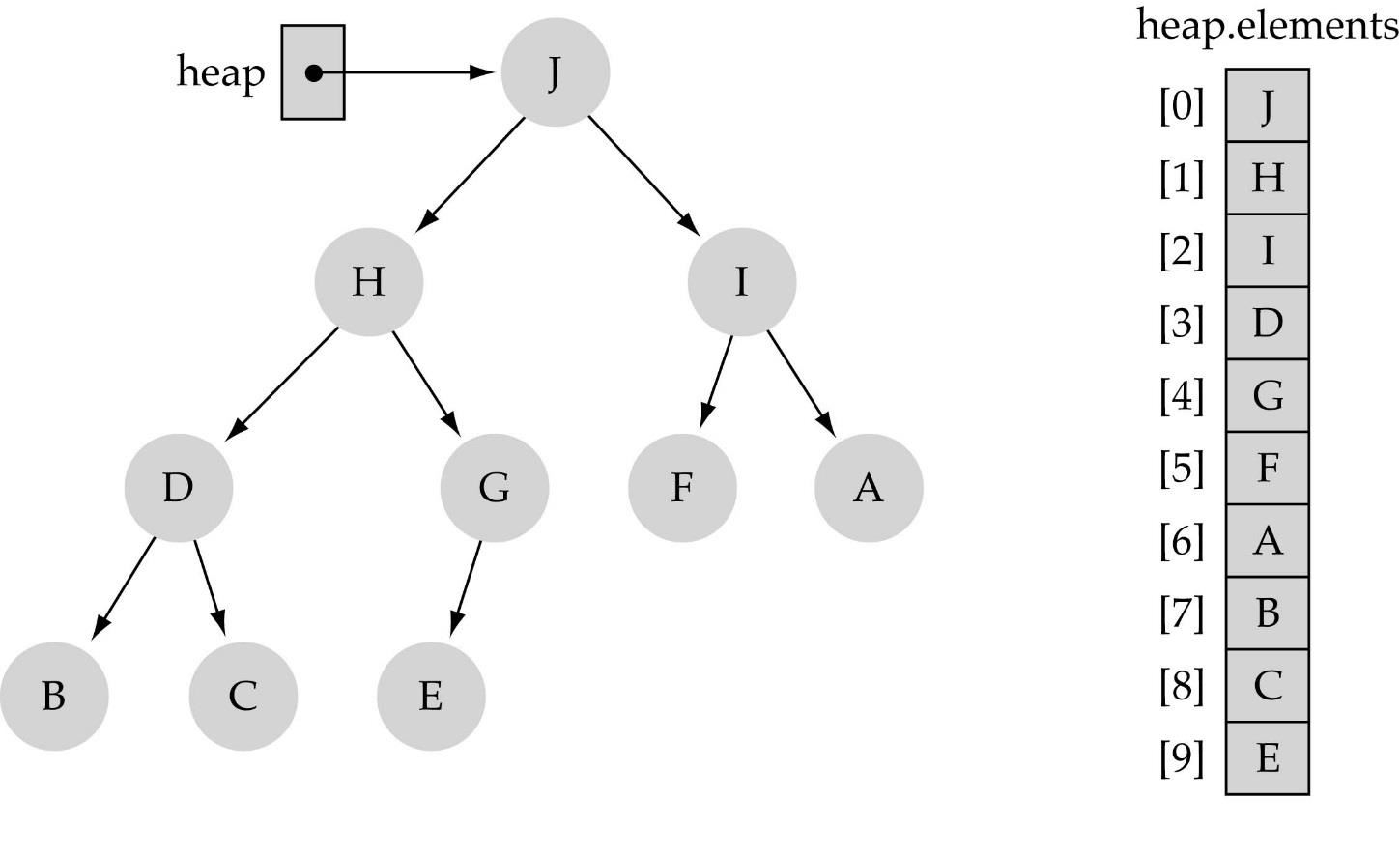
일반적으로 array로 tree를 구현했을 때 단점이 안쓰는 노드가 있으면 배열 중간에 비어있는 부분이 생기는데 heap의 경우 이러한 부분이 없기 때문에 문제가 없다.
이때 각각의 tree에서 array의 index로 할당하는 방법은 현재 노드가 tree.nodes [index]라면 왼쪽 자식 노드는 tree.nodes[index * 2 + 1]에 저장하면 되고, 오른쪽 자식 노드는 tree.nodes[index * 2 + 2]에 저장하고, 부모 노드는 tree.nodes[(index - 1) / 2]에 저장된다.
Heap조건이 안맞을 때
- ReheapDown
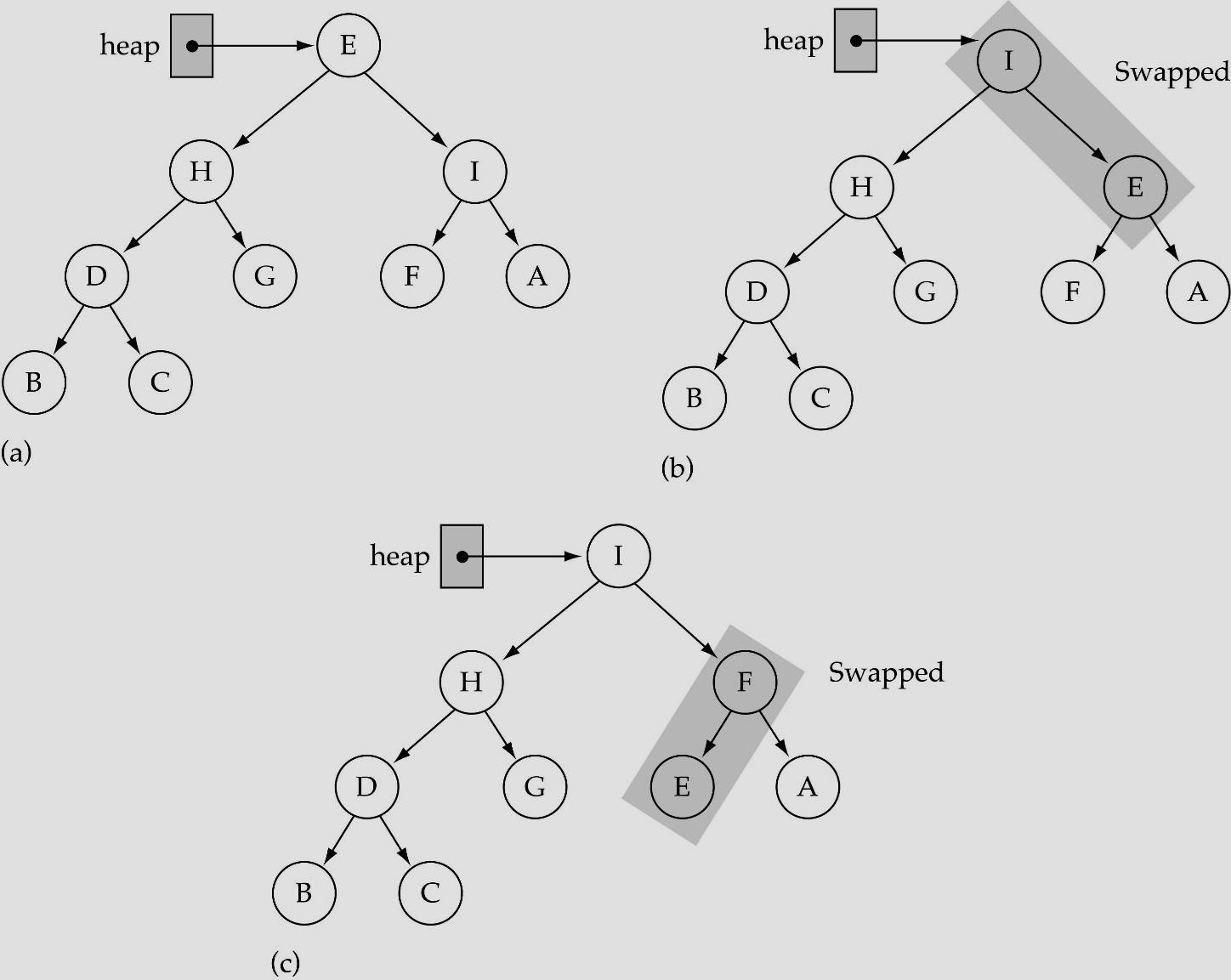
만약 부모 노드의 값이 더 작아서 heap조건이 깨졌으면 부모 노드의 값을 밑으로 내려서 다시 heap조건에 맞게 수정해야 한다.
이때 수정을 한 다음에는 heap조건을 만족해야 하기 때문에 문제가 생긴 노드의 자식 노드 중 큰 값을 부모 노드와 바꿔줘야 한다.
만약 값을 swap해준 뒤에도 문제가 발생하면 문제가 해결될 때까지 이 과정을 반복하여 heap조건을 모두 충족시키면 된다.
void Swap(ItemType& one, ItemType& two) {
ItemType temp;
temp = one;
one = two;
two = temp;
}
void ReheapDown(int root, int bottom) {
int maxChild;
int rightChild;
int leftChild;
leftChild = root * 2 + 1;
rightChild = root * 2 + 2;
if (leftChild <= bottom) { // basecase로 더 이상 자식 노드가 없는 경우
if (leftChild == bottom)
maxChild = leftChild;
else {
if (elements[leftChild] <= elements[rightChild])
maxChild = rightChild;
else
maxChild = leftChild;
}
if (elements[root] < elements[maxChild]) {
Swap(elements[root], elements[maxChild]);
ReheapDown(maxChild, bottom);
}
}
}leftChild가 bottom이면 자식 노드가 하나만 있다는 뜻이므로 해당 노드를 보면 되고, 자식 노드가 두 개이면 두 자식 노드중에서 큰 값을 가지고 있는 노드를 찾아 해당 위치를 확인하면 된다.
이렇게 찾은 위치의 노드의 값과 현재 노드의 값을 비교해 만약 현재 노드의 값이 더 작다면 heap조건에 맞게 하기 위해 두 값을 서로 바꿔주고 바꾼 자식 노드의 위치에서 함수를 다시 실행한다.
- ReheapUp
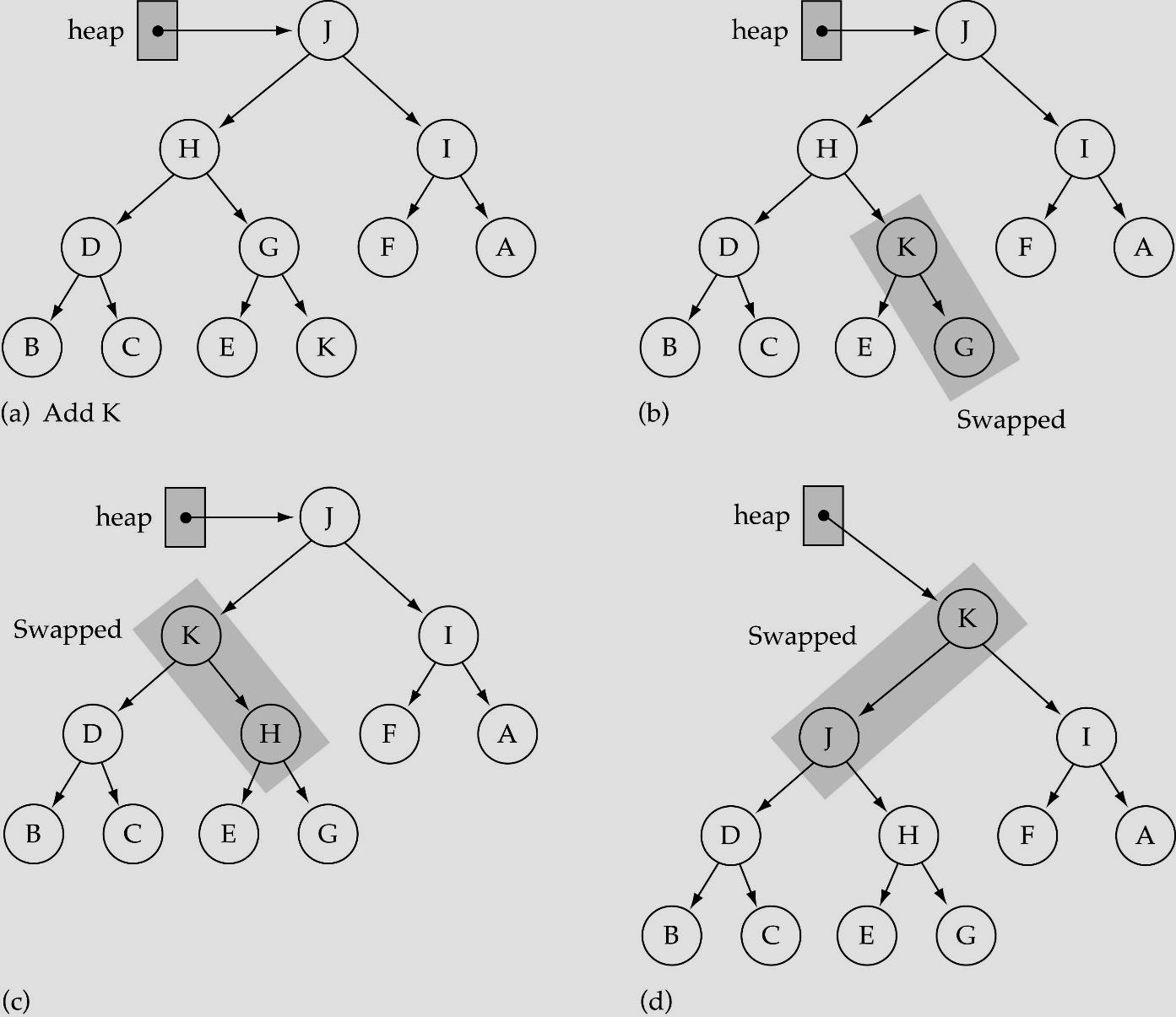
이와 반대로 부모 노드의 값이 더 커서 heap조건이 깨졌으면 부모 노드의 값을 위로 올려서 다시 heap조건에 맞게 수정해야 한다.
조건이 만족할 때까지 부모 노드와 현재 노드의 값을 계속 바꿔주면 된다.
void ReheapUp(int root, int bottom) {
int parent;
if (bottom > root) { //basecase 더 이상 부모 노드가 없는 경우
parent = (bottom - 1) / 2;
if (elements[parent] < elements[bottom]) {
Swap(elements[parent], elements[bottom]);
ReheapUp(root, parent);
}
}
}
parent의 index는 $\frac{(\text{자신의} index - 1)}{2}$ 이므로 해당 노드 위치의 값과 자신의 값을 비교해 만약 부모 노드의 값이 더 작다면 현재 노드의 값과 swap하고 부모 노드에서 다시 ReheapUp을 수행한다
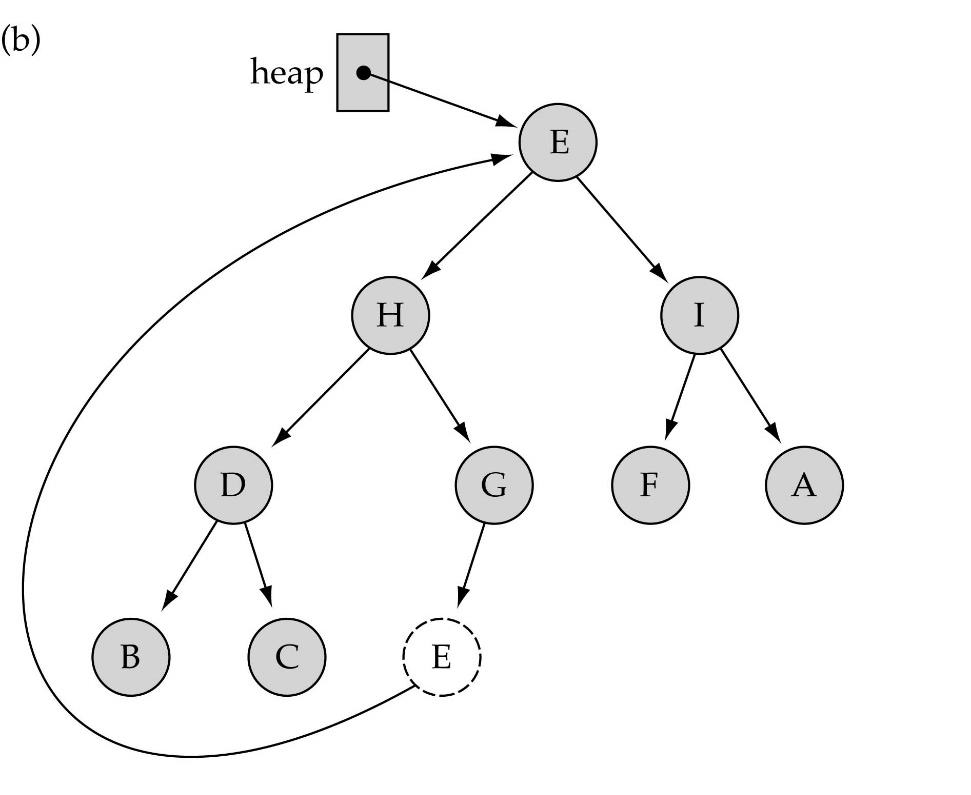
Delete
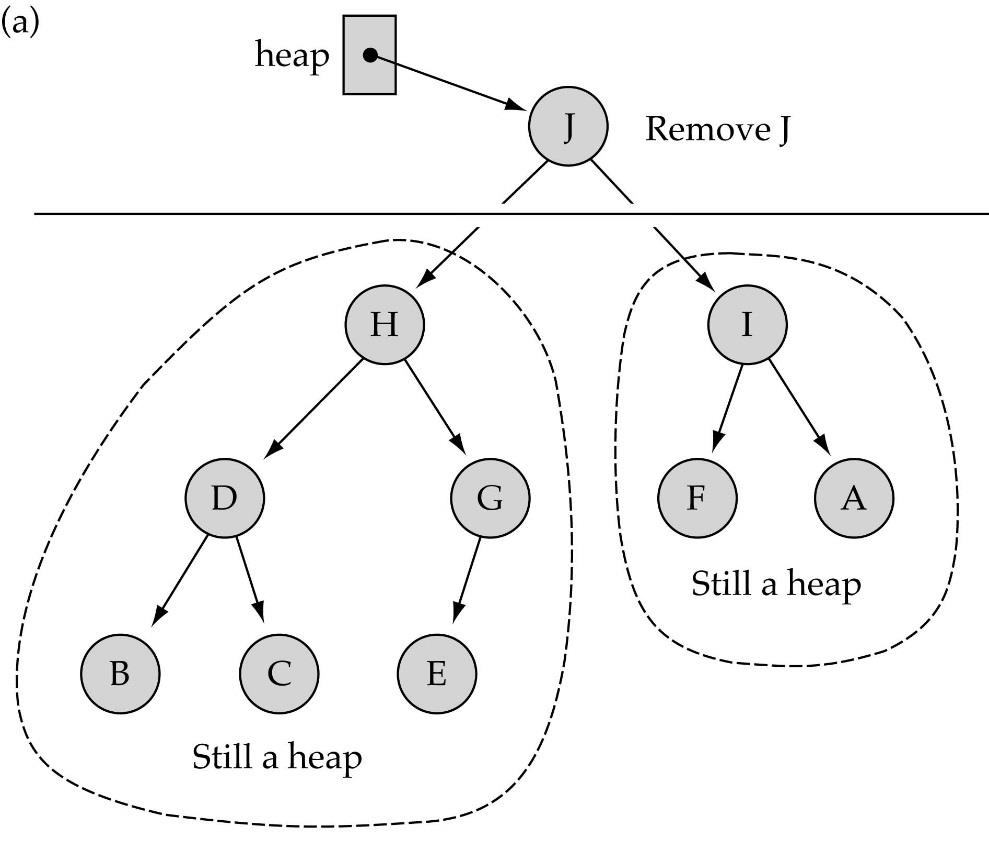
heap에서 가장 큰 원소 즉, root의 값을 지우게 된다면 heap에서 가장 마지막 노드에 있는 값을 root에 대입해주고 ReheapDown을 통해 깨졌던 heap의 조건을 다시 맞춰주면 된다.
만약 가장 큰 값이 아니더라도 이와 같은 방법으로 지우고 싶은 노드를 root로 생각했을 때 생기는 tree도 heap구조를 만족하기 때문에 해당 부분에서 이와 같은 방법을 똑같이 적용하면 된다.
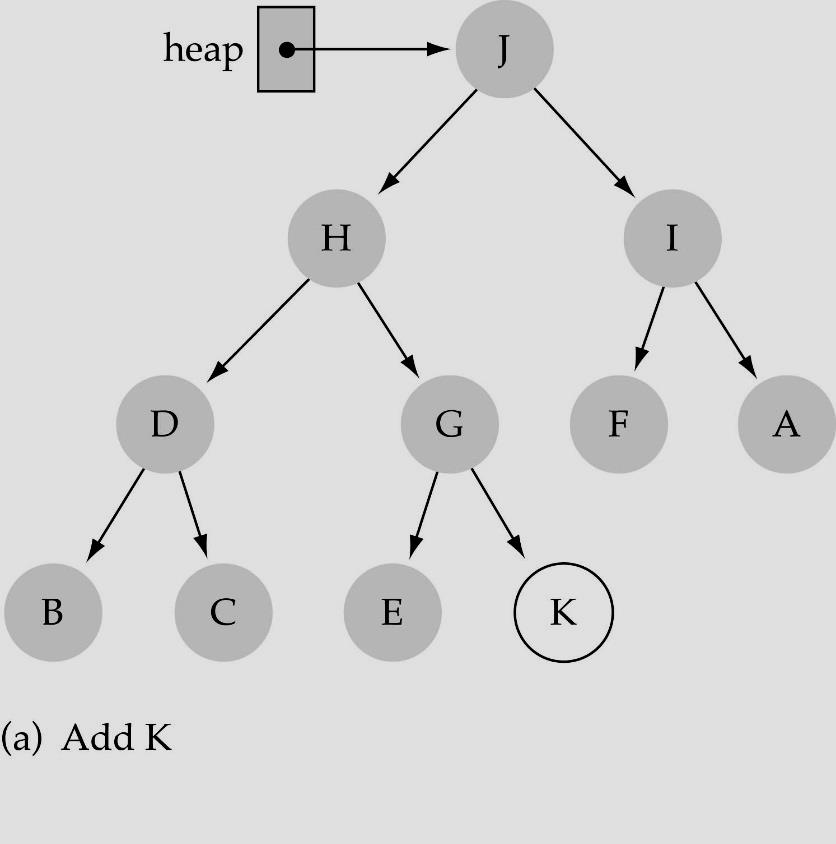
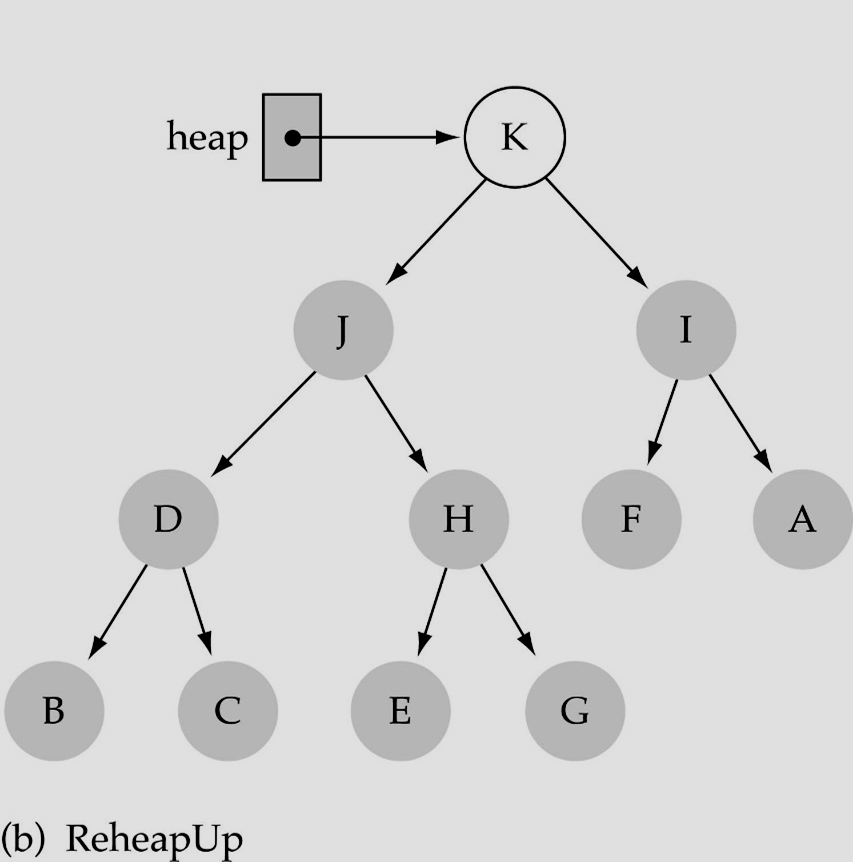
Insert
heap에 원소를 추가하게 되면 complete binary tree를 만족하기 위해 가장 마지막 위치에 새로운 값을 삽입하고 ReheapUp을 통해서 heap구조를 다시 맞춰주면 된다.
NonRecursive
만약 ReheapDown이나 ReheapUp을 수행할 때 재귀를 사용하지 않고 구현하려면 while문을 사용해서 동일하게 수행해주면 된다.
void ReheapUp_NonRecursive(int root, int bottom) {
int parent;
bool reheaped = false;
while (bottom > root && !reheaped) {
parent = (bottom - 1) / 2;
if (elements[parent] < elements[bottom]) {
Swap(elements[parent], elements[bottom]);
bottom = parent;
}
else
reheaped = true;
}
}
void ReheapDown_NonRecursive(int root, int bottom) {
int maxChild, leftChild, rightChild;
bool reheapded = false;
leftChild = root * 2 + 1;
while (leftChild <= bottom && !reheapded) {
if (leftChild == bottom)
maxChild = leftChild;
else {
rightChild = leftChild + 1;
maxChild = (elements[leftChild] <= elements[rightChild]) ? rightChild : leftChild;
}
if (elements[root] <= elements[maxChild]) {
Swap(elements[root], elements[maxChild]);
root = maxChild;
leftChild = root * 2 + 1;
}
else
reheapded = true;
}
}'컴퓨터 > 자료구조' 카테고리의 다른 글
| 자료구조 - 그래프 (1) | 2023.11.30 |
|---|---|
| 자료구조 - 우선순위 큐(Priority Queue) (0) | 2023.11.29 |
| 자료구조 - 트리 (1) | 2023.11.28 |
| 자료구조 - Recursion(재귀) (2) | 2023.11.26 |
| 자료구조 - Linked List(Circular, Doubly Linked list) (2) | 2023.11.25 |

