IR언어는 각각의 tree마다 하나의 연산만을 표현한다.
예를들어 다음과 같은 연산의경우
MEM(BINOP(PLUS, TEMP(t), CONST(c)))아래의 그림과 같이 tree로 표현할 수 있다.
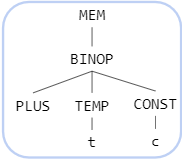
메로리 접근을 할 때 load/store instruction을 통해서 한다.
이때 각각의 명령어는 어떤 레지스터도 접근 가능하다.
그리고 레지스터 중에서 r0은 special register로 항상 0을 가진다.
각 명령어의 대기 시간은 한 사이클이고 이 한 사이클에 한 명령만 가능하다.
이제 기본적인 연산에 대해서 보면 다음과 같다.
ADD rd= rs1 + rs2 이는 기본적인 덧샘을 하는 연산이다.
ADDI rd= rs + c 이는 특별히 레지스터에 상수를 더해주는 연산이다.
SUB rd= rs1 – rs2 이는 기본적인 뺄샘을 하는 연산이다.
SUBI rd= rs – c 이는 특별히 레지스터에 상수를 빼주는 연산이다.
MUL rd= rs1 * rs2 이는 레지스터끼리 곱하는 연산이다.
DIV rd= rs1 / rs2 이는 레지스터끼리 나누는 연산이다.
그리고 메모리 연산에 대해서 보면 다음과 같다.
LOAD rd= M[rs + c] 이는 메모리의 값을 레지스터로 불러오는 연산이다.
STORE M[rs1 + c] = rs2 이는 레지스터 값을 메모리의 특정 위치로 저장하는 연산이다.
MOVEM M[rs1] = M[rs2] 이는 메모리의 특정 위치의 값을 다른 위치에 저장하는 연산이다.
그리고 우리는 직접 기계코드와 대응되지는 않는 연산인 Pseudo operation도 쓸 수 있다.
MOV rd= rs → ADDI rd= rs+ 0
MOV rd= rs → ADD rd= rs+ r0
MOV rd= c → ADDI rd= r0 + c
이는 위와 같이 0값 혹은 special register인 r0을 사용해서 move연산 대신 더하기 연산으로 값을 줄 수 있다.
위의 내용을 바탕으로 각각의 연산에 대해서 tree를 나타내면 아래와 같다.

이제 위의 표를 바탕으로 IR tree에서 해당하는 부분을 묶으면 아래와 같은 예시를 볼 수 있다.

이렇게 묶는다면 아래와 같이 총 10개의 연산과 9개의 레지스터를 사용해서 위의 IR tree를 표현 할 수 있다.
ADDI r1 ← r0 + offseta
ADD r2 ← r1 + FP
LOAD r3 ← M[r2 + 0]
ADDI r4 ← r0 + 4
MUL r5 ← r4 * ri
ADD r6 ← r3 + r5
ADDI r7 ← r0 + offsetx
ADD r8 ← r7 + FP
LOAD r9 ← M[r8 + 0]
STORE M[r6 + 0] ← r9
다만 이를 조금 수정하여 최소 비용이 드는 명령을 찾게 최적화를 진행 할 수 있다.
Maximal Munch Algorithm
root노드에서 시작하여 가장 큰 tile과 연결하는 탐욕적인 방법을 사용해서 최적화를 진행할 수 있다.
이러한 방법은 optimal tiling으로 국소적으로는 가장 좋은 방법을 찾지만 이게 가장 낮은 비용이라는 확신이 없다.
다만 이는 구현하기 더 쉽기 때문에 상황에 따라서 사용한다.

LOAD r3 ← M[FP + offseta]
ADDI r4 ← r0 + 4
MUL r5 ← r4 * ri
ADD r6 ← r3 + r5
ADD r8 ← FP + offsetx
MOVEM M[r6] ← M[r8]위의 tree를 maximal munch로 구현을 하면 위와같이 총 5개의 레지스터와 6개의 instruction으로 구현할 수 있다.
Dynamic Programming
subtree의 최적 결과를 합쳐서 가장 최적의 결과를 만드는 방법이다.
이는 기존의 DP와 동일하게 bottom up 방식으로 동작을 하고 아래와 같이 동작하는데 각각의 노드에 대해서 앞에는 최소 비용을 적고 뒤에는 표에서 대응되는 패턴을 적는다.

그리고 아래의 노드에서 구한 결과들을 이용해서 가장 최적의 비용을 구할 수 있다.
'컴퓨터 > 컴파일러' 카테고리의 다른 글
| 10. Register Allocation (4) | 2024.07.23 |
|---|---|
| 9. Liveness Analysis (2) | 2024.07.22 |
| 7. Basic Blocks and Traces (2) | 2024.07.19 |
| 6. Translation to Intermediate Code (2) | 2024.07.19 |
| 5. Activation Records (2) | 2024.07.18 |



