회귀
예측 변수를 통해 목표하는 데이터의 수치를 예측하는 문제이다.
분류에서 사용했던 K-NN알고리즘을 이용해서 동일한 원리로 예측하려는 샘플에 가장 가까운 샘플 K개를 선택하여 해당 샘플의 평균을 구하여 예측 타깃값을 정하면 된다.
결정계수
분류 문제의 경우 훈련 결과를 평가할 때 테스트 세트에 있는 샘플을 정확히 분류한 개수의 비율인 정확도를 사용해서 평가하였다.
하지만 회귀의 경우 정확히 맞다 아니다라고 할 수 없기 때문에 다른 평가 기준을 세워야하는데 그 점수를 결정계수라고 한다.
$$R^2 = 1 - \frac{\sum\limits_{i = 1}^n (y_i - \hat y_i )^2}{\sum\limits_{i = 1}^n (y_i - \mu )^2} \quad y_i: 실제값, \hat y_i : 예측값, \mu : 평균값$$
결정 계수는 위와 같이 정의하는데 이는 $1 - \frac{\text잔차의 분산}{\text종속변수의 분산}$으로 값이 1에 가까울수록 예측에 가까워진다는 뜻이다.
과대적합과 과소적합
- 과대적합
모델이 훈련 데이터에는 너무 잘 맞지만 일반성이 떨어지는 것으로, 이는 주로 데이터의 잡음의 양에 비해 모델이 너무 복잡할 때 발생한다.
따라서 파라미터수가 적은 모델을 사용하거나, 특성의 수를 줄이거나, 모델에 규제를 가하거나, 데이터 수를 늘리거나, 데이터의 노이즈를 제거하여 일반적인 경우에 더 맞게 하는 것을 사용하면 된다. - 과소적합
모델이 너무 단순해서 데이터의 내재된 구조를 학습하지못하는 경우이다.
이 경우는 위와 반대로 파라미터가 더 많은 모델을 쓰거나, 알고리즘에 특성을 좋은것으로 바꾸거나 모델의 규제를 줄이는 방법을 사용한다.
K-NN의 한계
K-NN의 경우 가장 인접한 데이터에 의해서 값이 결정되기 때문에 데이터가 분포하고 있는 영역 밖의 부분의 데이터나 데이터 세트와는 이질적인 데이터에는 제대로 된 예측을 할 수가 없다.
실제로 농어의 데이터가 아래와 같이 있다고 했을 때 새로운 데이터가 초록색으로 주워졌다고 하면 최근접 이웃은 항상 노란색으로 표시된 데이터에 해당하게 된다.
따라서 길이가 무엇이 되든 상관 없이 항상 무게가 동일하게 예측이 되고 이는 큰 오차를 발생시킨다.
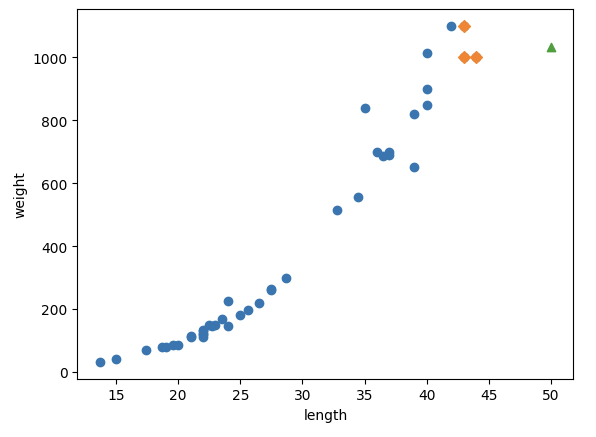

따라서 이러한 문제가 발생하기 때문에 K-NN을 사용하여 회귀 문제를 푸는 것은 적절하지 않다.
선형 회귀
널리 사용되는 대표적인 회귀 알고리즘으로 입력특성의 가중치 합과 편향을 더해 예측을 만든다.
$\hat y = \Theta_0 + \Theta_1x_1 + \Theta_2x_2 + … + \Theta_nx_n$
여기서 $\hat y$는 예측값, n의 특성의 수 $x_i$는 i번째 특성값이고 $\Theta_j$는 j번때 모델 파라미터이다.
scikit-learn의 LinearRegression을 이용하면 선형 회귀를 쉽게 구현할 수 있는데 이를 이용해 위처럼 농어가 50cm인 경우와 100cm인 경우를 그려보면 아래와 같다.


이를 보면 대략적인 추세는 맞지만 길이가 작은 농어의 경우 오차가 크게 발생하여 적절하게 예측에 성공했다고 하기 힘들다.
다항 회귀
가지고 있는 데이터가 비선형 데이터일 경우 선형 모델로 학습하기 위해서는 각 특성의 거듭제곱을 새로운 특성으로 추가하고 이 확장된 특성을 포함한 데이터셋에 선형모델을 훈련시키는 것이다.
2차 방정식에 해당하는 모델을 찾기 위해서는 각각의 데이터를 제곱한 항을 훈련 세트에 추가하고 학습을 해야한다.
따라서 이를 이용해 농어가 50cm인 경우와 100cm인 경우를 그려보면 아래와 같다.


대부분의 길이에서 큰 오차 없이 모든 데이터를 잘 표현하였고 훈련 세트와 테스트 세트의 결정계수를 비교해 봐도 점수가 높게 나와 예측을 잘 했음으로 알 수 있다.
다중 회귀
다중 회귀는 독립 변수가 2개 이상인 회귀 분석을 뜻하는 것으로 선형 회귀와 동일한 방법으로 진행된다.
규제
특성의 개수가 크게 늘어날 경우 선형 모델은 매우 강력해져 훈련 세트에 대해서 거의 완벽하게 학습할 수 있다.
하지만 노이즈에 대해서도 학습이 되어 과대적합할 가능성이 있다.
따라서 이러한 문제를 해결하기 위해서 모델이 훈련 세트를 너무 과도하게 학습하지 못하도록 규제라는 방법을 사용할 수 있다.
- 릿지 회귀
$$ J(\Theta) = MSE(\Theta) + \alpha {1 \over 2} { \sum_{i=1}^n \Theta_i^2} $$
이는 모델의 가중치가 가능한 작게 유지되려고 노력한다.
여기서 Alpha는 모델을 얼마나 많이 규제할지 조절하는 것으로 Alpha의 값이 크면 규제 강도가 세지므로 계수 값을 더 줄이고 더 과소적합되도록 유도한다.
규제가 작으면 그냥 선형 회귀와 같아지고, 규제가 크면 모든 가중치가 거의 0에 가까워져 데이터의 평균을 지나는 수평선이 된다.
- 라쏘 회귀
$$ J(\Theta) = MSE(\Theta) + \alpha \sum_{i=1}^n |\Theta_i| $$
라쏘 회귀의 경우 계수의 크기를 아예 0으로 만들 수 있어 결과적으로 라쏘회귀는 덜 중요한 특성의 가중치를 제거한다.
따라서 라쏘회귀는 자동으로 특성을 선택하고 희소모델을 만든다
'컴퓨터 > 머신러닝' 카테고리의 다른 글
| [혼자 공부하는 머신러닝] 5. 트리 알고리즘 (1) | 2024.02.18 |
|---|---|
| [혼자 공부하는 머신러닝] 4. 다양한 분류 알고리즘 (1) | 2024.02.10 |
| [혼자 공부하는 머신러닝] 1. 나의 첫 머신러닝 & 2. 데이터 다루기 (1) | 2024.01.30 |
| PRML 2. 확률 분포 (0) | 2023.11.08 |
| PRML 1. 기본적인 머신러닝 소개 (0) | 2023.11.04 |


