Linked List를 이용하여 Unsorted List를 봐보겠다.
Unsorted이기 때문에 Insert의 경우 stack에서 구현된 것처럼 그냥 제일 앞에 new로 새로운 노드를 만들어주고 해당 노드의 다음 값으로 원래 가장 앞에 있던 노드를 지목해 주면 된다.
하지만 Delete의 경우도 기존의 방식처럼 지우고 싶은 값을 찾다가 해당 값이 나오는 노드를 지워주는 방식을 사용하면 연결된 리스트가 중간에 끊기는 경우가 발생해 버린다.
따라서 지워야 할 노드가 생기면 이전 노드의 다음 연결된 주소를 지워야 하는 노드의 다음 노드로 연결해줘야 하는데 단일 연결 리스트의 경우 찾고자 하는 값이 있는 노드에 오게 되면 이전 노드의 위치를 알 수가 없어 이러한 과정이 불가능하다.
따라서 이전 노드를 가리키는 포인터를 따로 만들거나 현제 노드의 값을 비교하는 것이 아니라 다음 노드의 값이 찾는 값이 맞는지 비교하여 만약 찾는 값이라면 지금 노드의 다음 노드를 다음다음 노드로 연결해 주는 과정을 수행해야 한다.
따라서 후자인 경우를 생각해 보면 내가 찾는 값 item == (location->next)->info인 경우 location->next = ( location->next )->next로 해주면 된다.
다만 다음의 값만 비교하면 리스트의 가장 앞의 값은 비교해 볼 수 없으므로 이때만 예외사항으로 처리해 주면 된다.
class UnsortedType {
NodeType* listData;
int length;
NodeType* currentPos;
public:
UnsortedType();
~UnsortedType();
bool IsFull() const;
int LengthIs() const;
void MakeEmpty();
void RetrieveItem(ItemType& item, bool& found);
void InsertItem(ItemType item);
void DeleteItem(ItemType item);
void ResetList();
void GetNextItem(ItemType& item);
};
UnsortedType::UnsortedType() {
length = 0;
listData = NULL;
}
UnsortedType::~UnsortedType() {
MakeEmpty();
}
bool UnsortedType::IsFull() const {
NodeType* location;
try {
location = new NodeType;
delete location;
return false;
}
catch (bad_alloc exception) {
return true;
}
}
int UnsortedType::LengthIs() const {
return length;
}
void UnsortedType::MakeEmpty() {
NodeType* tempPtr;
while (listData != NULL) {
tempPtr = listData;
listData = listData->next;
delete tempPtr;
}
length = 0;
}
void UnsortedType::RetrieveItem(ItemType& item, bool& found) {
bool moreToSearch;
NodeType* location;
location = listData;
found = false;
moreToSearch = (location != NULL);
while (moreToSearch && !found) {
if (item == location->info) {
found = true;
item = location->info;
}
else {
location = location->next;
moreToSearch = (location != NULL);
}
}
}
void UnsortedType::InsertItem(ItemType item) {
NodeType* location;
location = new NodeType;
location->info = item;
location->next = listData;
listData = location;
length++;
}
void UnsortedType::DeleteItem(ItemType item) {
NodeType* location = listData;
NodeType* tempLocation;
if (item == listData->info) {
tempLocation = location;
listData = listData->next;
}
else {
while (!(item == (location->next)->info))
location = location->next;
tempLocation = location->next;
location->next = (location->next)->next;
}
delete tempLocation;
length--;
}
void UnsortedType::ResetList() {
currentPos = NULL;
}
void UnsortedType::GetNextItem(ItemType& item) {
if (currentPos == NULL)
currentPos = listData;
else
currentPos = currentPos->next;
item = currentPos->info;
}
이제 Linked List를 이용하여 Sorted List를 봐보자.
기존의 Sorted List는 정렬되있다는 장점을 통해 리스트 속의 특정 값을 찾을 때 이분탐색을 이용해 빠르게 찾을 수 있었다.
하지만 Linked List의 경우 중간위치까지 한 번에 갈 수가 없어 순차적으로 이동해서 가야하기 때문에 이러한 방법이 의미가 없다.
따라서 Sorted와 Unsorted의 delete과정이 동일하다.
다만 Sorted이기 때문에 Insert과정에서 적절한 위치를 찾고 해당 위치에 삽입을 해야한다.
이때 delete에서 사용한 방식처럼 다음 다음의 값과 비교하여 삽입할 위치를 결정하게 된다면 마지막 노드의 다음 노드는 없기 때문에 만약 새로 삽입해야할 요소가 가장 마지막에 삽입되어야 한다면 에러가 발생하게 된다.
이러한 문제를 해결하기 위해서 이전 노드를 가리키는 포인터를 따로 만드는 전자의 방법을 생각해 볼 수 있다.
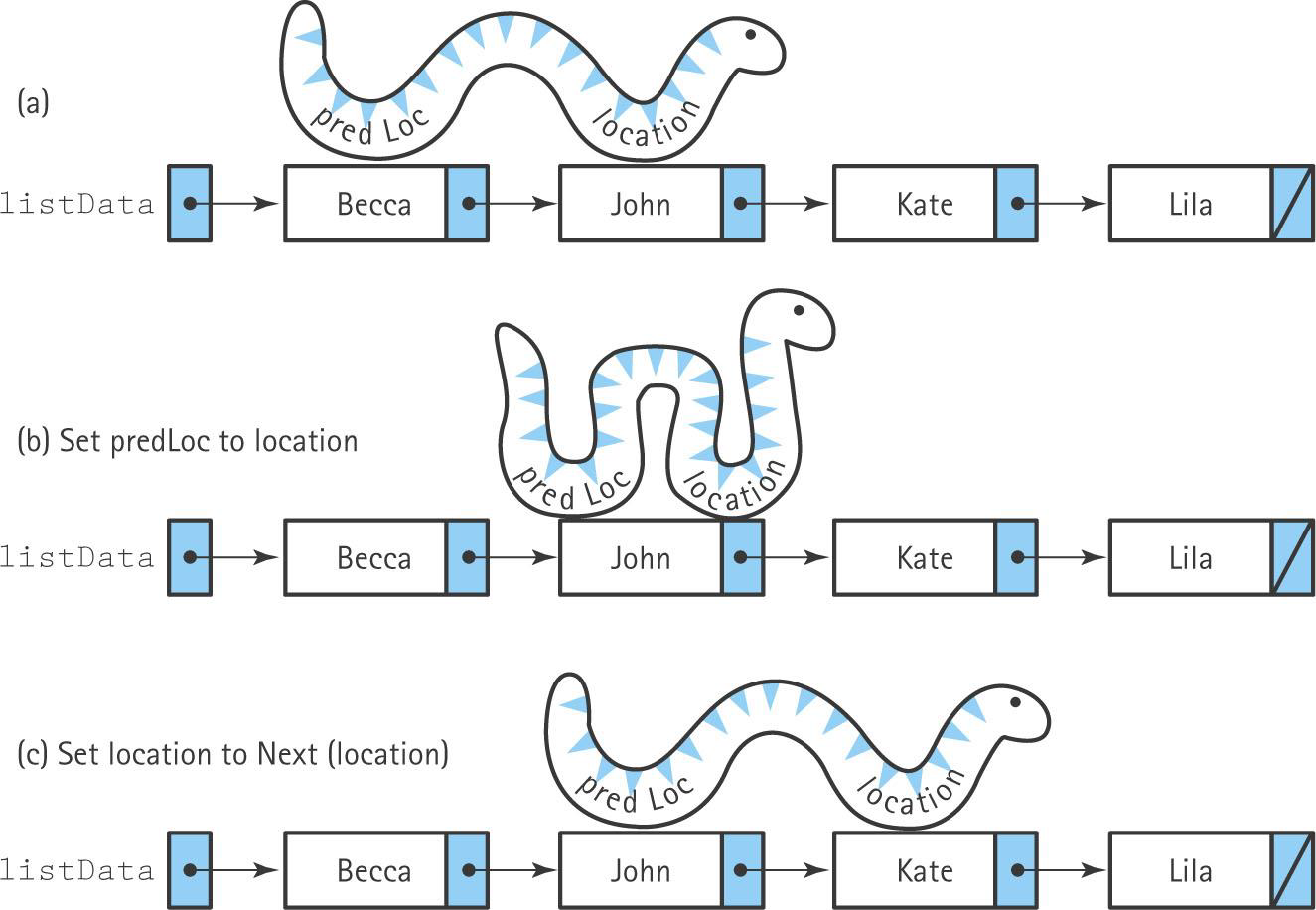
이전 노드를 가리키는 포인터와 현재 노드를 가리키는 포인터가 있을 때 이전 노드를 가리키는 포인터를 먼저 현재 노드의 위치로 이동하고 현재 노드를 가리키는 포인터를 다음 노드로 이동시키는 방식으로 나아가면서 노드의 원소와 삽입할 원소를 비교해야하는데 만약 현재 노드를 먼저 이동할 경우 이전 노드에서 다음 노드로 이동할 방법이 없기 때문이다.
이때 이전 predLoc->next로 다음 노드로 이동하면 안되는 이유는 리스트 탐색 초기상태에 location은 listData를 가리키고 있고 predLoc은 NULL인데 이 경우에는 다음 노드가 없기 때문에 예외처리를 따로 또 해줘야 하는 불편함이 있기 때문이다.
이제 이런 식으로 노드를 이동하면서 적절한 위치를 찾게 된다면 predLoc->next를 new로 생성한 삽입해야할 노드로 지정해주고, 새로운 노드와 location을 연결해주면 된다.
이제 이러한 내용을 바탕으로 Sorted List를 구현해보면 다음과 같다.
class SortedType {
NodeType* listData;
int length;
NodeType* currentPos;
public:
SortedType();
~SortedType();
bool IsFull() const;
int LengthIs() const;
void MakeEmpty();
void RetrieveItem(ItemType& item, bool& found);
void InsertItem(ItemType item);
void DeleteItem(ItemType item);
void ResetList();
void GetNextItem(ItemType&);
};
SortedType::SortedType() {
length = 0;
listData = NULL;
}
SortedType::~SortedType() {
NodeType* tempPtr;
while (listData != NULL) {
tempPtr = listData;
listData = listData->next;
delete tempPtr;
}
}
bool SortedType::IsFull() const {
NodeType* location;
try {
location = new NodeType;
delete location;
return false;
}
catch (bad_alloc exception) {
return true;
}
}
int SortedType::LengthIs() const {
return length;
}
void SortedType::MakeEmpty() {
NodeType* tempPtr;
while (listData != NULL) {
tempPtr = listData;
listData = listData->next;
delete tempPtr;
}
length = 0;
}
void SortedType::RetrieveItem(ItemType& item, bool& found) {
bool moreToSearch;
NodeType* location;
location = listData;
found = false;
moreToSearch = (location != NULL);
while (moreToSearch && !found) {
if (location->info < item) {
location = location->next;
moreToSearch = (location != NULL);
}
else if (item == location->info) {
found = true;
item = location->info;
}
else
moreToSearch = false;
}
}
void SortedType::InsertItem(ItemType item) {
NodeType* newNode;
NodeType* predLoc;
NodeType* location;
bool moreToSearch;
location = listData;
predLoc = NULL;
moreToSearch = (location != NULL);
while (moreToSearch) {
if (location->info < item) {
predLoc = location;
location = location->next;
moreToSearch = (location != NULL);
}
else
moreToSearch = false;
}
newNode = new NodeType;
newNode->info = item;
if (predLoc == NULL) {
newNode->next = listData;
listData = newNode;
}
else {
newNode->next = location;
predLoc->next = newNode;
}
length++;
}
void SortedType::DeleteItem(ItemType item) {
NodeType* location = listData;
NodeType* tempLocation;
if (item == listData->info) {
tempLocation = location;
listData = listData->next;
}
else {
while (!(item == (location->next)->info))
location = location->next;
tempLocation = location->next;
location->next = (location->next)->next;
}
delete tempLocation;
length--;
}
void SortedType::ResetList() {
currentPos = NULL;
}
void SortedType::GetNextItem(ItemType& item) {
if (currentPos == NULL)
currentPos = listData;
item = currentPos->info;
currentPos = currentPos->next;
}
'컴퓨터 > 자료구조' 카테고리의 다른 글
| 자료구조 - Recursion(재귀) (2) | 2023.11.26 |
|---|---|
| 자료구조 - Linked List(Circular, Doubly Linked list) (2) | 2023.11.25 |
| 자료구조 - Linked List(Stack & Queue) (1) | 2023.11.23 |
| 자료구조 - Queue (2) | 2023.11.22 |
| 자료구조 - 메모리 할당 (0) | 2023.11.21 |


